CUDA series: Part 3 — CUDA Memory
Published:
More Explanation on Warp
Continuing from the previous part covering the basic of CUDA programming, let’s start this part by diving deep into an important component, Warp.
GPU does not schedule work to each thread individually. Instead, it groups threads in the same thread block into several units called warps. According to NVIDIA design, each warp contains exactly 32 CUDA threads. Please be aware that the CUDA thread is not the same as an operating system thread! CUDA threads are lighter than OS threads, and managed by the GPU hardware and CUDA runtime instead of OS.
If a kernel is launched with 1024 threads per block, the GPU will organize them into 32 warps because there is 32 threads per warp and 1024/32=32. The warp scheduler, which is a hardware unit within each SM, then issues one common instruction for all 32 threads in a warp.
There are two questions that can occur here.
- What happen if a thread block size is less than 32 threads?
- How warps can help the GPU executes the program faster?
For the first question, the GPU still allocates 32 threads for the warp, but the remaining threads in the warp will be inactive or masked off. This reduces efficiency because you do not fully utilize the hardware. Therefore, as a rule of thumb, you should always set a size of thread block to be a multiple of 32 unless you have a strong reason (like extremely small grids). You can read more here.
For the second question, it hides the latency. Okay, this deserves more explanation.
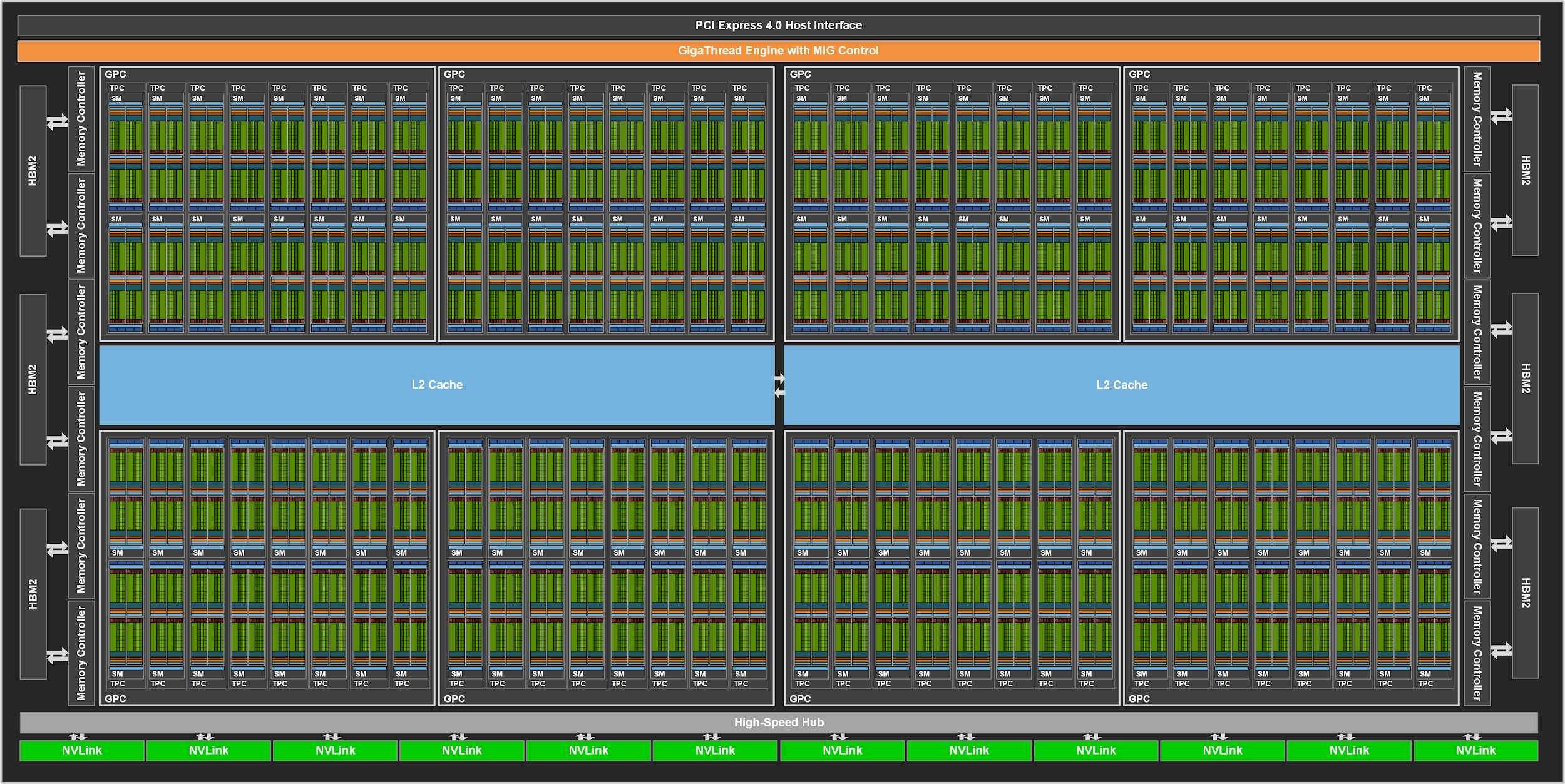GA100 Full GPU with 128 SMs. The A100 Tensor Core GPU has 108 SMs. Ref: NVIDIA
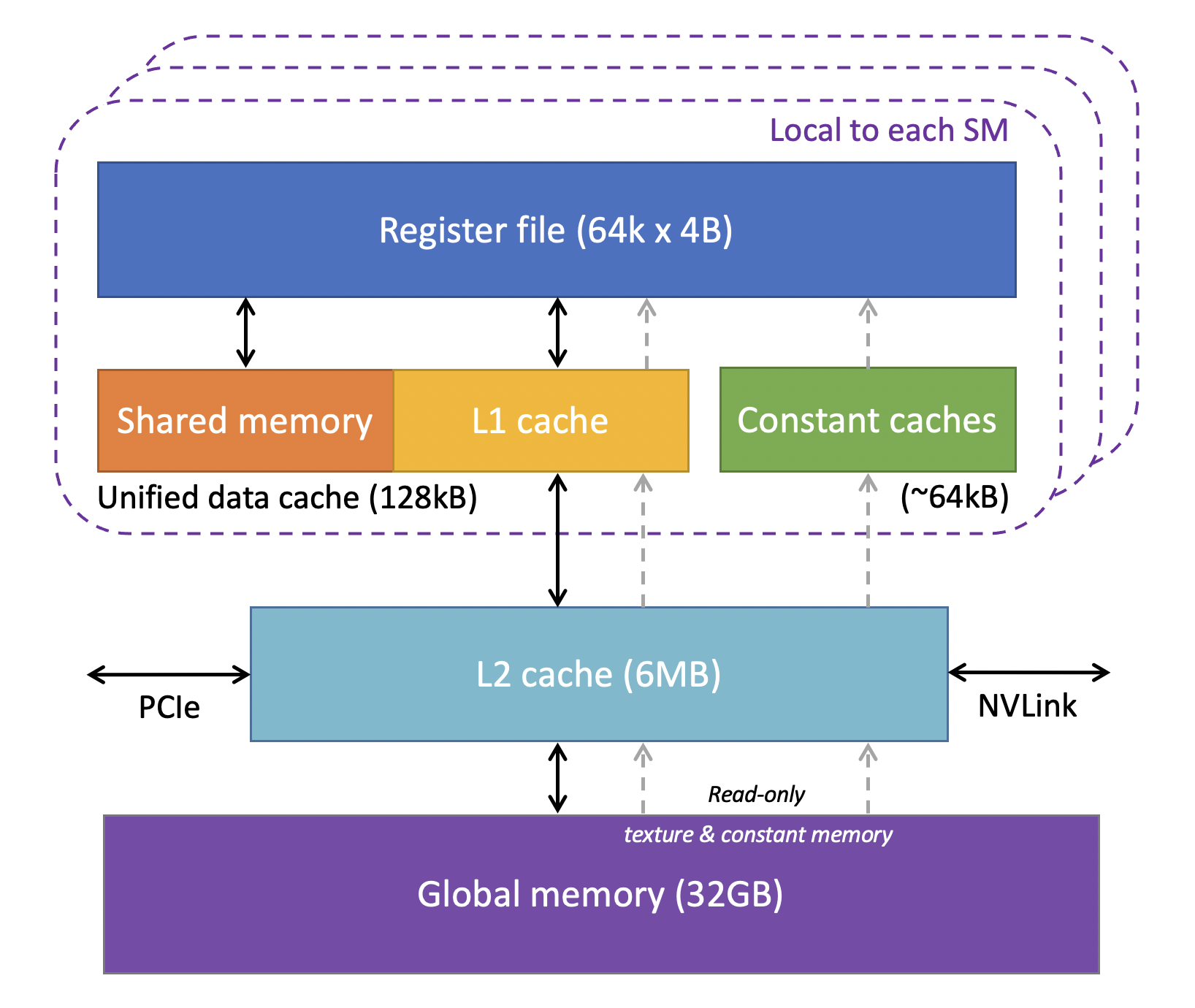GPU Memory Hierarchy Ref: Cornell
When the thread wants to access data from a GPU global memory, it has to wait for a large number of cycles. In CPU, it uses some techniques such as having a big cache, which is not a case in the GPU, and Out-of-Order execution, which is unavailable in the GPU. Instead, the GPU uses a massive multithreading method. It ensures that it can work on another warp to work while waiting the current warp to access data.
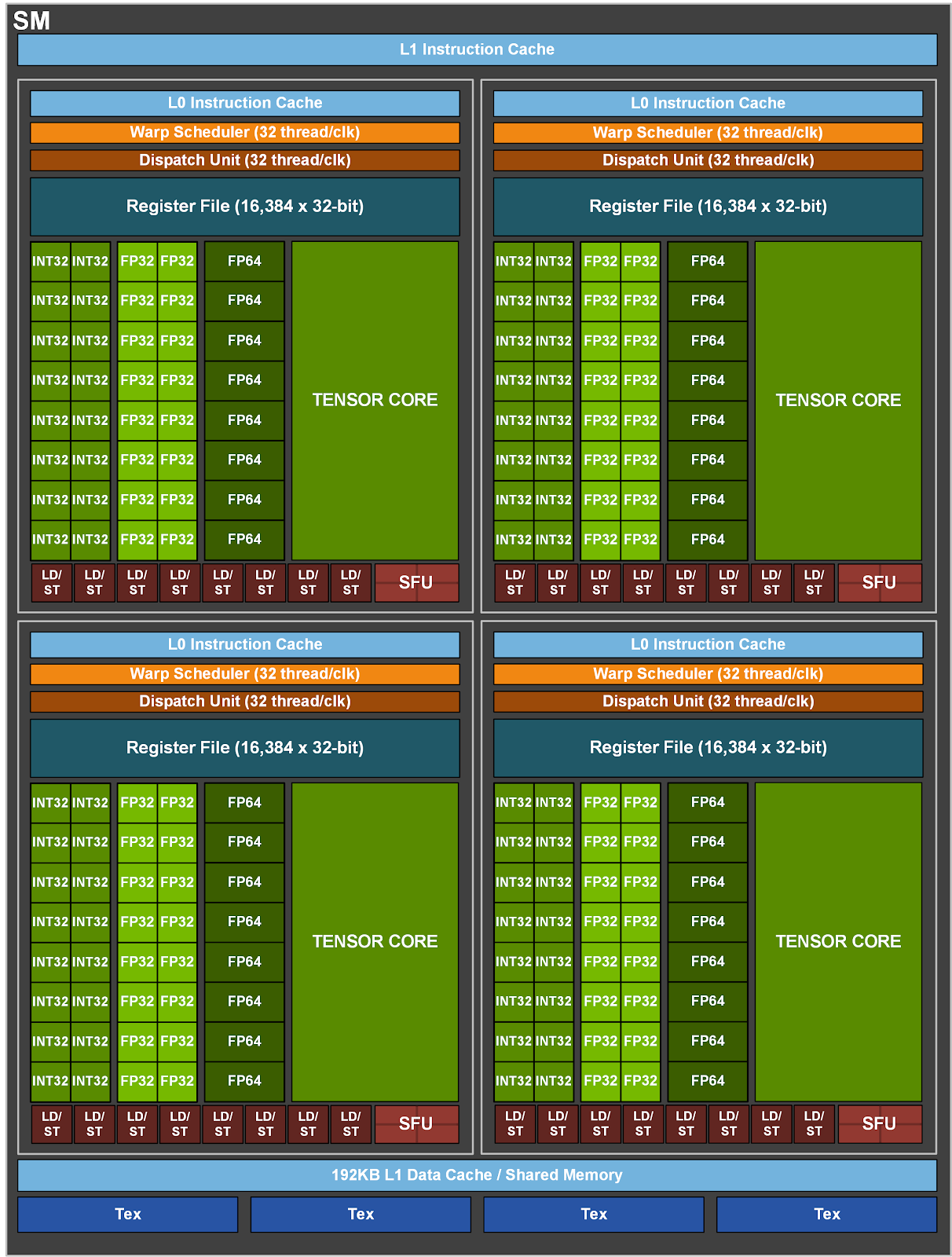The GA100 streaming multiprocessor (SM). Ref: NVIDIA
For example, let’s imagine that the warp 1 executing in a particular SM needs to access data from the global memory. The warp 1 goes into a waiting state while accessing the data from the memory. While waiting for the first warp, the SM’s warp scheduler, as you see from the The GA100 streaming multiprocessor (SM) image, then immediately switches to execute the warp 2. Then, the warp 2 needs to access data from the global memory as well. This warp goes into a waiting state. The SM’s warp scheduler then immediately switches to execute the warp 3. And so on. The scheduler switches among warps as long as there is at least one ready warp.
However, if all active warps stall, the SM idles until one of these warps becomes ready. For example, when the warp 1 finishes getting data from the global memory, its execution is then resumed. After the warp 1 finishes its works, the scheduler picks another warp changing back to a ready state, if available, to be executed. This happens repeatedly until all warps are executed.
As long as there are enough active warps to schedule, the GPU can keep the SM busy and hide latency. While the first warp waits for its data, the GPU works on another warp. This is how the GPU hides its latency. It does not make the memory access faster, but it keeps the GPU constantly busy with different work.
So, here are some takeaways of the GPU allocation.
- A thread block contains many CUDA threads.
- An SM may run more than one block.
- A block can only be scheduled to one SM.
- We, as a developer, cannot choose which SM to send a block to.
- Threads within a block are grouped into warp(s), which each warp has 32 threads.
- GPU Scheduling uses this warp unit to hide a memory access latency.
CUDA Memory Layout
Broadly, we classify memory as on-chip (registers, shared memory, caches) and off-chip (global, local, constant, texture). When we are talking about them, we refer to their physical location of memory relative to the GPU cores.
On-chip memory locates near to the GPU cores. As a result, the cores can access data on this memory extremely fast. Off-chip memory is a separate memory that is connected to the GPU through high-speed buses. Accessing data from this off-chip memory is slow since data needs to travel for a long distance.
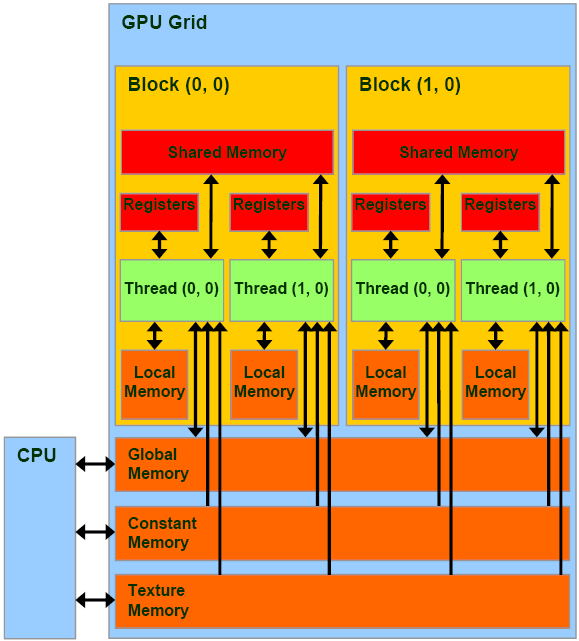
CUDA Memory Model. Ref: 3DGEP
Registers are the fastest storage, directly accessed by instructions. To access it, you only need a variable declaration. Be aware that the number of registers per block is limited. If you exceed the register allocated per thread, the compiler moves to local memory (off-chip).
__global__ void registerExample() {
float a = 5.0f; // Stored in on-chip registers
float b = threadIdx.x; // Stored in on-chip registers
float result = a * b; // Computation using on-chip registers
}
Shared memories are an on-chip memory that each of them is shared by several threads in a particular thread block. It can be accessed extremely fast as well; therefore, you can copy data from a global memory to this shared memory so that all threads in this thread block can accessed them fast. But you must be aware of its small size. The variables that use this shared memory are annotated by __shared__.
__global__ void sharedMemoryExample() {
__shared__ float cache[256]; // Stored in on-chip shared memory
int tid = threadIdx.x;
cache[tid] = tid * 2.0f; // Fast on-chip access
__syncthreads();
float value = cache[tid]; // Fast on-chip access
}
Global memory is an off-chip memory. It is slower to be accessed comparing to the registers and the shared memories, but it is a lot larger. Data accessed from this memory will be cached in L1 (if available) and L2 cache. This is the location that the host can read and write data to by using cudaMemcpy.
__global__ void globalMemoryExample(float *data) {
int tid = threadIdx.x;
float value = data[tid]; // Off-chip access: take hundreds of cycles
}
My personal note: Constant memory is still missing here. Don’t forget to add them here.
Local memory is an off-chip memory. Despite its name, local memory is not local or fast. It is essentially global memory used for thread-private data that does not fit in registers.
__global__ void localMemoryExample() {
int tid = threadIdx.x;
// These will likely be in REGISTERS (fast)
float a = 5.0f;
float b = tid * 2.0f;
float c = a + b;
// These will likely be in LOCAL MEMORY (slow)
float large_array[1000]; // Too large for registers
int dynamic_index = tid % 100;
float indexed_array[100];
indexed_array[dynamic_index] = 5.0f; // Runtime indexing forces local memory
// Accessing local memory (slow as global memory!)
for (int i = 0; i < 1000; i++) {
large_array[i] = i * 2.0f;
}
float result = large_array[dynamic_index]; // Another slow access
}
An Example Showing the Benefit of Using the Shared Memory
The shared memory deserves more explanation! This memory can be looked as a scratchpad memory. Developers can load data that will be frequently used to here. You should not load unnecessary data to be here since its size is small. Only threads within a particular thread block can access each shared memory. Its data lifetime is the same as the block’s lifetime.
This is a square matrix multiplication program. I will name it as shared_memory_test.cu. A kernel matrix_mult_global does the multiplication on the global memory, while matrix_mult_shared copies partial data of an array A and B into the shared memory and later access data from the shared memory to compute the multiplication.
#include <cuda_runtime.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Use the global memory
__global__ void matrix_mult_global(float *A, float *B, float *C, int N) {
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
if (row < N && col < N) {
float sum = 0.0f;
for (int k = 0; k < N; k++) {
sum += A[row * N + k] * B[k * N + col]; // Multiple global memory accesses
}
C[row * N + col] = sum;
}
}
// Use the shared memory
__global__ void matrix_mult_shared(float *A, float *B, float *C, int N) {
__shared__ float As[16][16]; // allocate the matrix on the shared mem with the size of 16*16
__shared__ float Bs[16][16]; // allocate the matrix on the shared mem with the size of 16*16
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
float sum = 0.0f;
for (int tile = 0; tile < (N + 15) / 16; tile++) {
// Load tiles into shared memory
if (row < N && (tile * 16 + threadIdx.x) < N) {
As[threadIdx.y][threadIdx.x] = A[row * N + tile * 16 + threadIdx.x];
} else {
As[threadIdx.y][threadIdx.x] = 0.0f;
}
if ((tile * 16 + threadIdx.y) < N && col < N) {
Bs[threadIdx.y][threadIdx.x] = B[(tile * 16 + threadIdx.y) * N + col];
} else {
Bs[threadIdx.y][threadIdx.x] = 0.0f;
}
// You must wait for all threads to copy data into the shared mem before computing the multiplication
__syncthreads();
// Compute using shared memory
for (int k = 0; k < 16; k++) {
sum += As[threadIdx.y][k] * Bs[k][threadIdx.x];
}
__syncthreads();
}
if (row < N && col < N) {
C[row * N + col] = sum;
}
}
int main() {
const int N = 512; // Smaller for clearer demonstration
size_t size = N * N * sizeof(float);
float *h_A, *h_B, *h_C_global, *h_C_shared;
float *d_A, *d_B, *d_C_global, *d_C_shared;
// Allocate host memory
h_A = (float*)malloc(size);
h_B = (float*)malloc(size);
h_C_global = (float*)malloc(size);
h_C_shared = (float*)malloc(size);
// Initialize matrices
for (int i = 0; i < N * N; i++) {
h_A[i] = (float)rand() / RAND_MAX;
h_B[i] = (float)rand() / RAND_MAX;
}
// Allocate device memory
cudaMalloc(&d_A, size);
cudaMalloc(&d_B, size);
cudaMalloc(&d_C_global, size);
cudaMalloc(&d_C_shared, size);
// Copy to device
cudaMemcpy(d_A, h_A, size, cudaMemcpyHostToDevice);
cudaMemcpy(d_B, h_B, size, cudaMemcpyHostToDevice);
dim3 blockSize(16, 16);
dim3 gridSize((N + 15) / 16, (N + 15) / 16);
// Timing
cudaEvent_t start, stop;
cudaEventCreate(&start);
cudaEventCreate(&stop);
printf("Matrix multiplication: %dx%d\n", N, N);
printf("Block size: 16x16, Grid size: %dx%d\n\n", gridSize.x, gridSize.y);
// Time global memory version
cudaEventRecord(start);
for (int i = 0; i < 10; i++) {
matrix_mult_global<<<gridSize, blockSize>>>(d_A, d_B, d_C_global, N);
}
cudaEventRecord(stop);
cudaEventSynchronize(stop);
float global_time;
cudaEventElapsedTime(&global_time, start, stop);
global_time /= 10;
// Time shared memory version
cudaEventRecord(start);
for (int i = 0; i < 10; i++) {
matrix_mult_shared<<<gridSize, blockSize>>>(d_A, d_B, d_C_shared, N);
}
cudaEventRecord(stop);
cudaEventSynchronize(stop);
float shared_time;
cudaEventElapsedTime(&shared_time, start, stop);
shared_time /= 10;
// Copy results back
cudaMemcpy(h_C_global, d_C_global, size, cudaMemcpyDeviceToHost);
cudaMemcpy(h_C_shared, d_C_shared, size, cudaMemcpyDeviceToHost);
// Check correctness
bool correct = true;
float max_diff = 0.0f;
for (int i = 0; i < N * N && correct; i++) {
float diff = fabs(h_C_global[i] - h_C_shared[i]);
max_diff = fmax(max_diff, diff);
if (diff > 1e-3) correct = false;
}
printf("Performance Results:\n");
printf("==================\n");
printf("Global Memory Time: %.3f ms\n", global_time);
printf("Shared Memory Time: %.3f ms\n", shared_time);
printf("Speedup: %.2fx\n", global_time / shared_time);
printf("Results match: %s (max diff: %.6f)\n", correct ? "Yes" : "No", max_diff);
if (shared_time < global_time) {
printf("\n✓ Shared memory is %.2fx faster!\n", global_time / shared_time);
}
cudaEventDestroy(start);
cudaEventDestroy(stop);
cudaFree(d_A); cudaFree(d_B); cudaFree(d_C_global); cudaFree(d_C_shared);
free(h_A); free(h_B); free(h_C_global); free(h_C_shared);
return 0;
}
To run this script, run nvcc -o shared_memory_test shared_memory_test.cu, then ./shared_memory_test.
Let’s go into the detail of how matrix_mult_shared kernel works.
Basically, this kernel gives each thread to work on computing each element of the array C. For example, there is a thread computing C[0][0], and there is another thread computing C[0][1], and so on.
When calling this kernel from the host, we have to determine the number of thread blocks and the thread block size in matrix_mult_shared<<<gridSize, blockSize>>>.
I decide that each thread block has 256 threads that is aligned as a shape of 16x16. It is determined by dim3 blockSize(16, 16). In this example, block size of 16x16 is chosen to match the tile size on the shared memory. If you change the block shape, you must also adjust how data is loaded into shared memory and change the allocated matrix size on the shared memory.
We can determine the number of thread blocks by dim3 gridSize((N+15) / 16, (N+15) / 16). The reason that it is (N+15) / 16 because C++ always round down the decimal. For example, let’s assume that we have a full matrix size of 15x15. If we use N/15, 15/16 will give 0, which means that no thread block will be given. This is an undesired behavior because we still need 1 thread block for handling 15 threads. As a result, we add 15 to ensure that there is enough thread block to handle all threads. In our example, (15+15)/16 will give 1. Hooray! These 15 threads have a thread block. In general, the formula will be (N+(M-1))/M where N is the number of threads and M is the size of each thread block.
Now, let’s go into the implementation detail of matrix_mult_shared. First, we declare two arrays having a size of 16x16 in the shared memory for storing partial copies of the array A and B. Because each thread block has its own shared memory, if there is more than one thread block, each shared memory relating to each thread block will be allocated As and Bs. Therefore, all shared memories used by thread blocks will have these two matrices allocated.
__shared__ float As[16][16];
__shared__ float Bs[16][16];
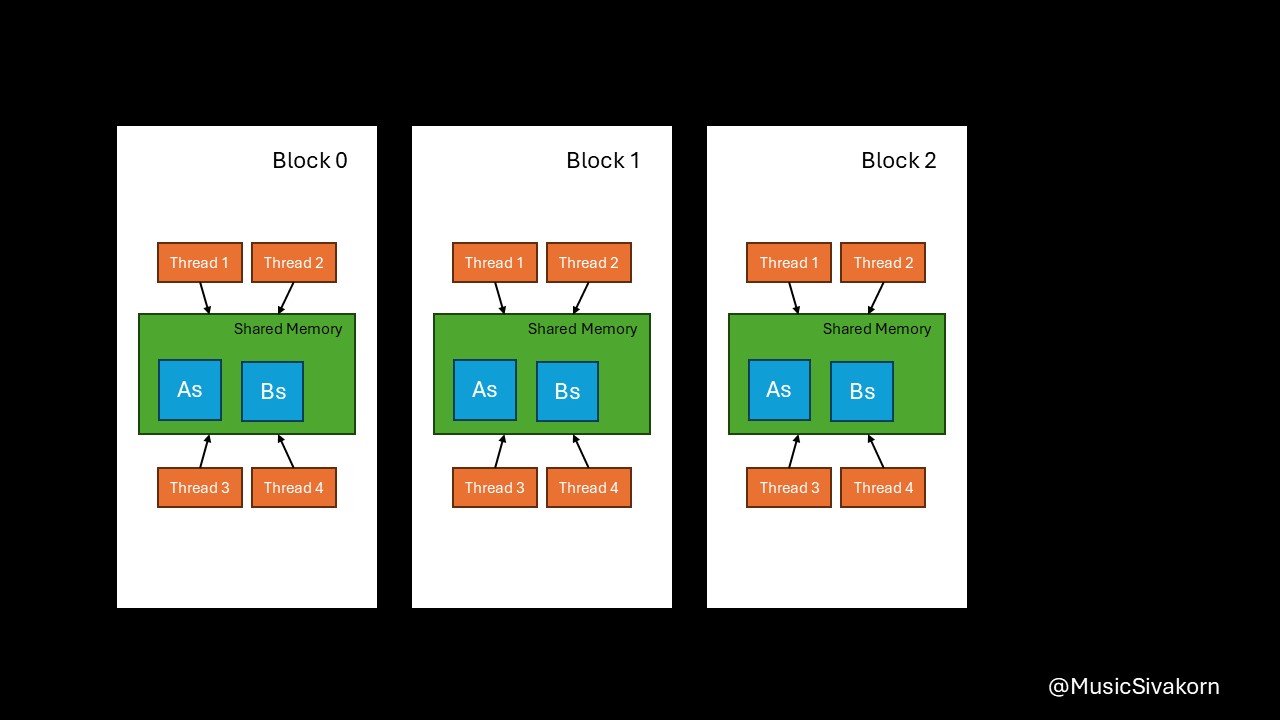Every thread block has its own shared memory.
The important point of this program is that each thread is responsible for one element in the array C. Because of this, we can fix the value of row and column for each thread. As a result, each thread knows which row and column of the original matrix A and B they need to work on. For example, the thread with row=0 and column=0 knows that it must use the row 0 of the array A and the column 0 of the array B to compute C[0][0], and the thread with row=5 and column=10 knows that it must use the row 5 of the array A and the column 10 of the array B to compute C[5][10], and so on.
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
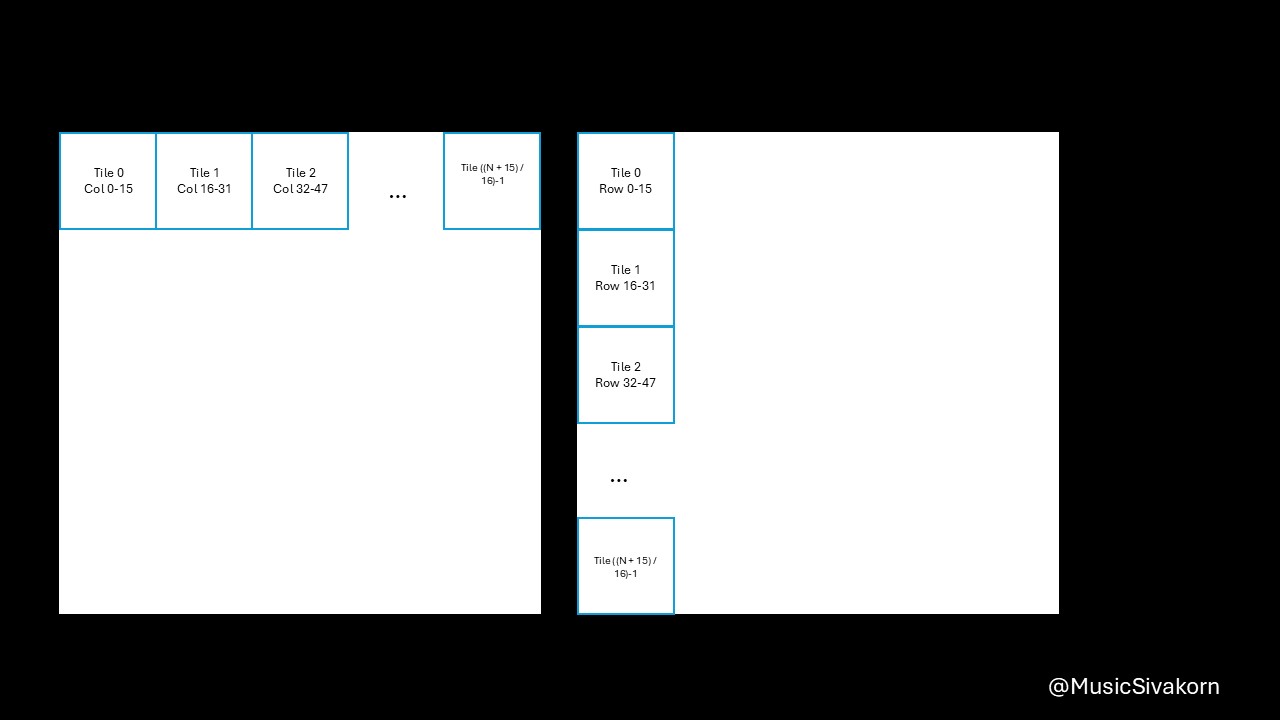
Then, it goes into a loop for (int tile = 0; tile < (N + 15) / 16; tile++) {...}. As an overview explanation, we can only compute the partial result of 16 elements at a time because our shared memory size is 16x16. So, how it works is that the variable sum has the partial multiplication result of the first 16 elements of the array A (A[0..15]) and B (B[0..15]) after finishing the first iteration (tile=0). Then, it will have the partial multiplication result of the first 32 elements of the array A and B after finishing the second iteration (tile=1) by adding the multiplication result of element A[16..31] and B[16..31] to the current sum having the result of the first 16 elements, and so on.
for (int tile = 0; tile < (N + 15) / 16; tile++) {
...
}
Now, let’s go into detail of this loop.
For data copying, the idea is that each thread copies only one element from the A and B to As and Bs.
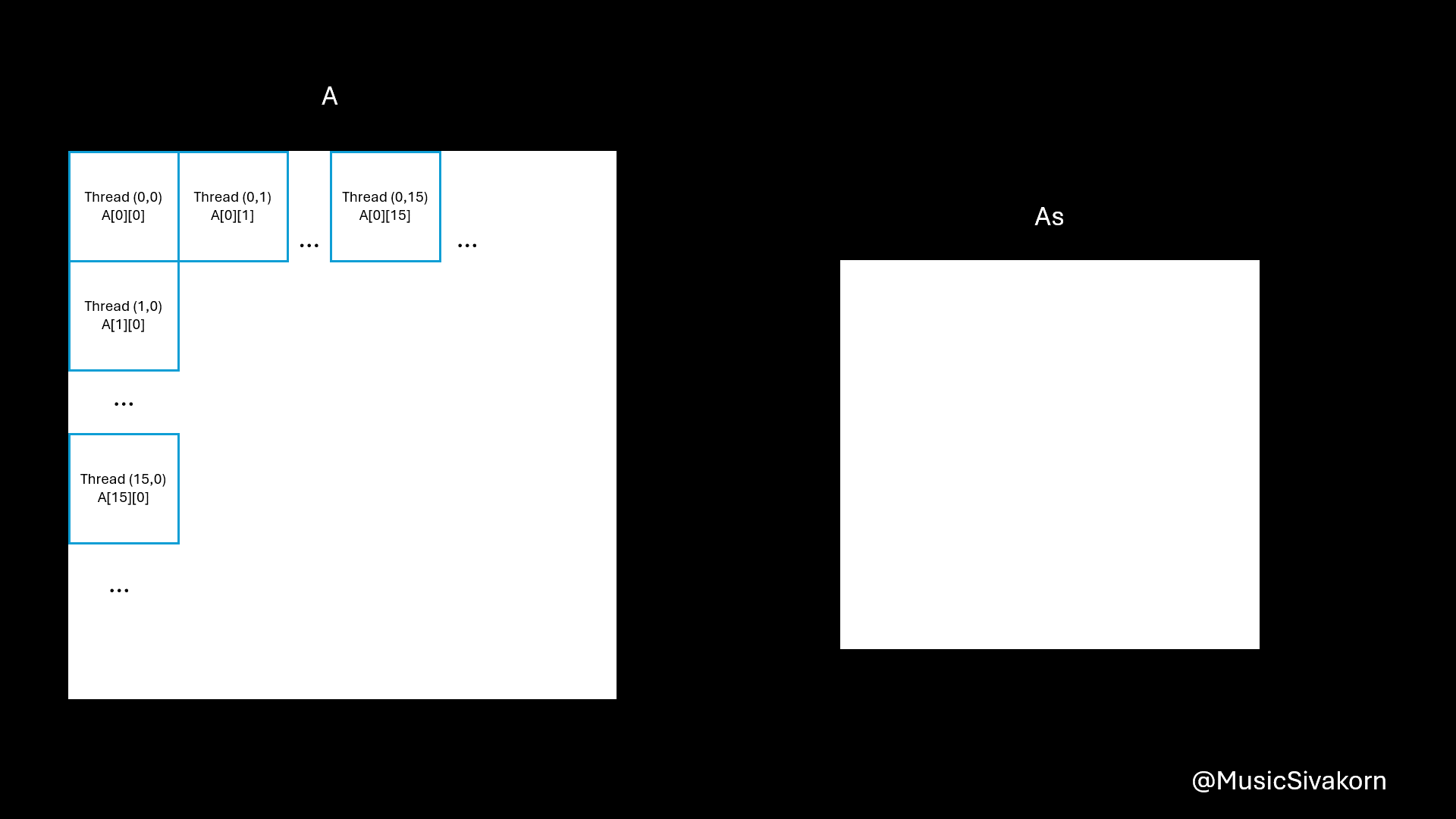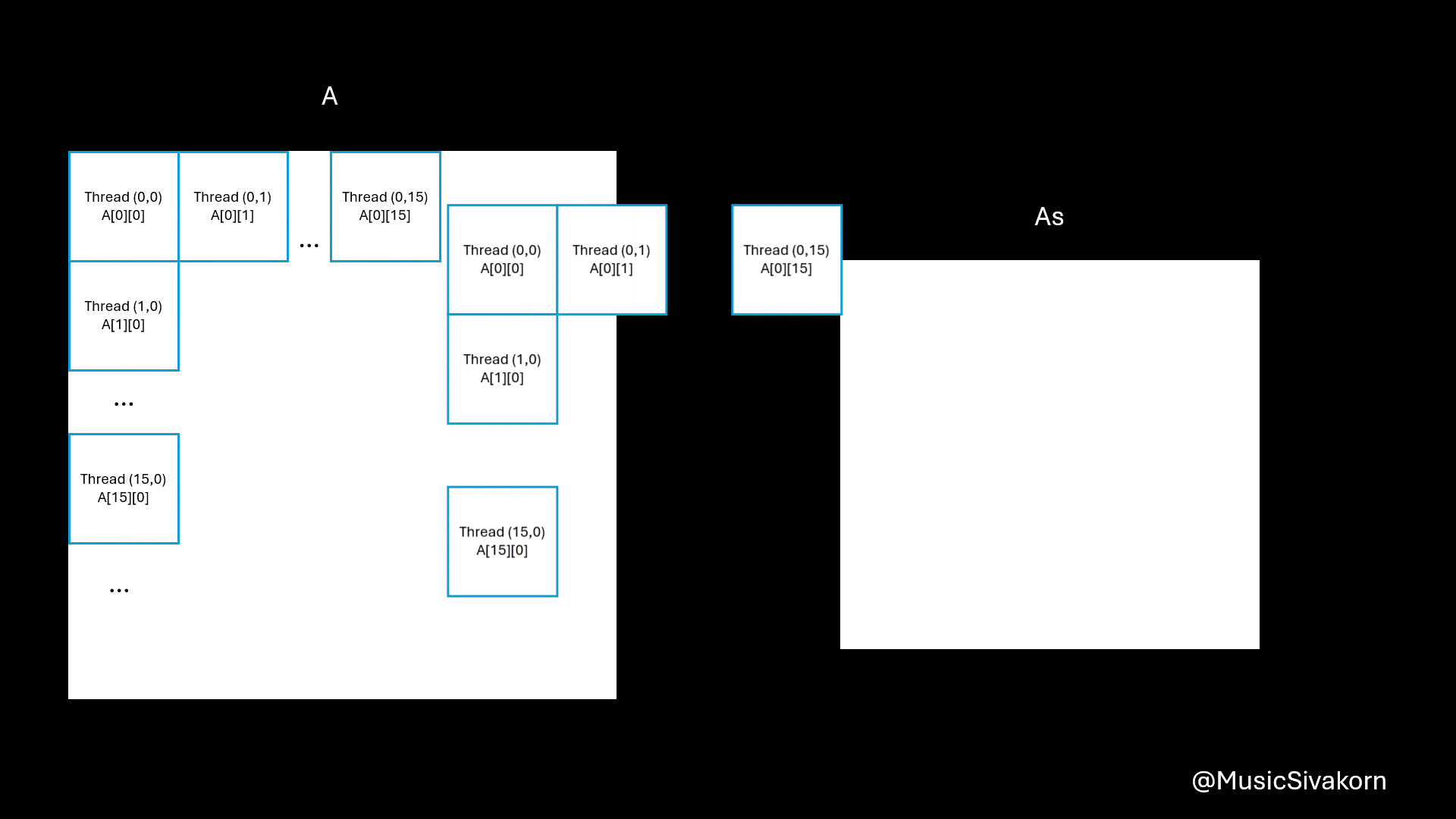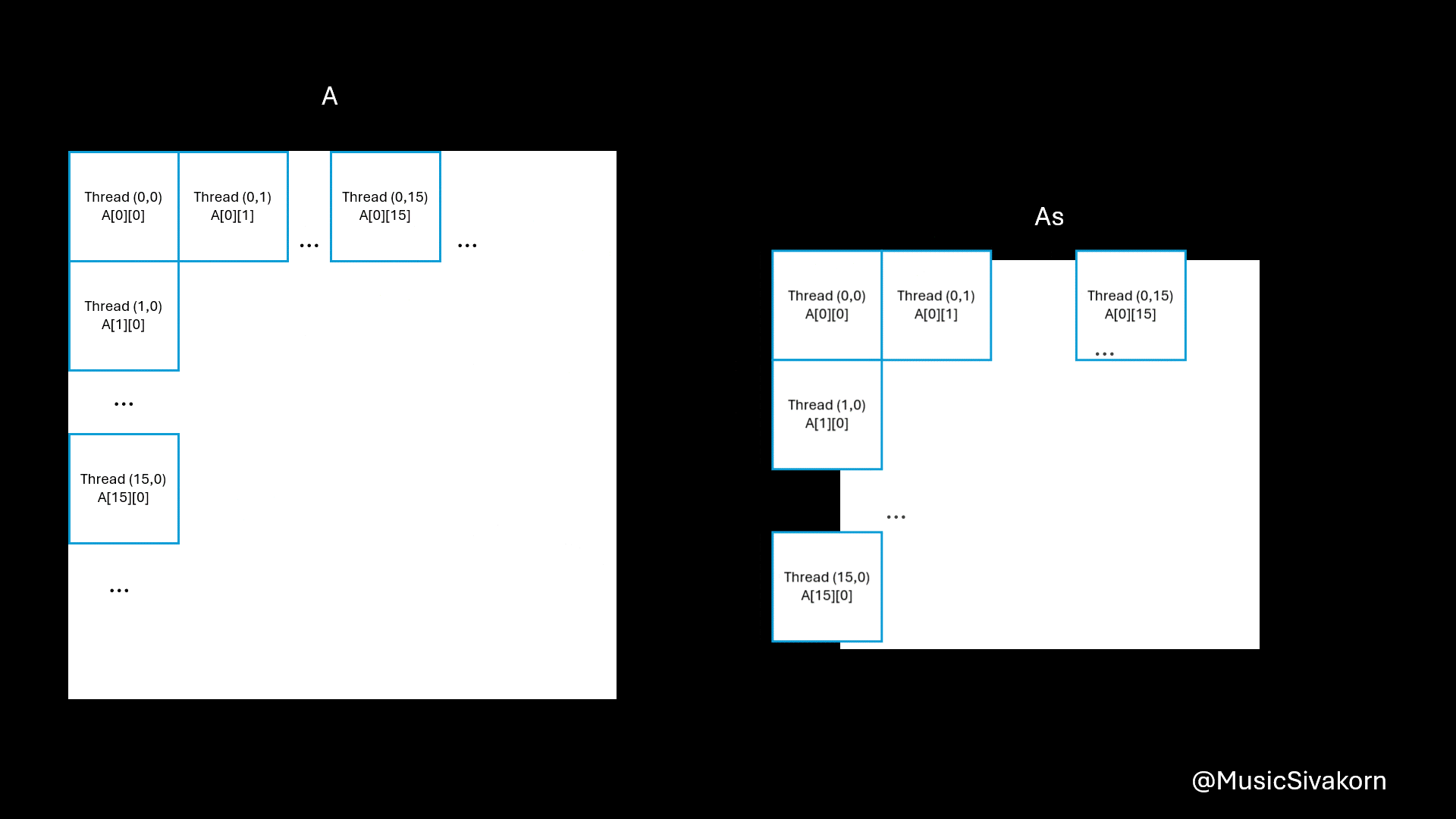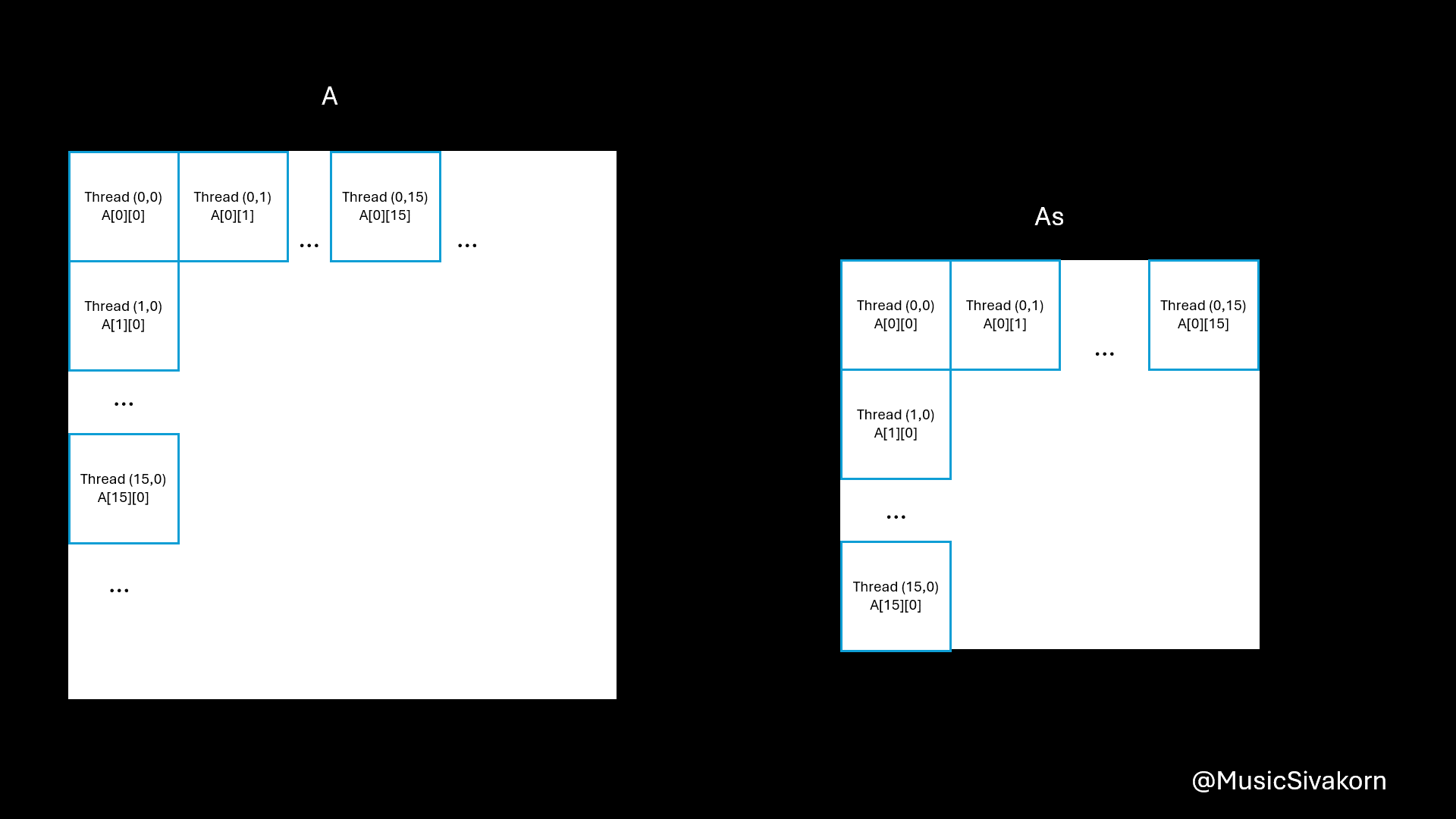
// Still inside the tile loop
if (row < N && (tile * 16 + threadIdx.x) < N) {
As[threadIdx.y][threadIdx.x] = A[row * N + tile * 16 + threadIdx.x];
} else {
As[threadIdx.y][threadIdx.x] = 0.0f;
}
if ((tile * 16 + threadIdx.y) < N && col < N) {
Bs[threadIdx.y][threadIdx.x] = B[(tile * 16 + threadIdx.y) * N + col];
} else {
Bs[threadIdx.y][threadIdx.x] = 0.0f;
}
Because blockSize is 16x16, the value of threadIdx.x and threadIdx.y is from 0 to 15, inclusive.
The reasons of being A[row * N + tile * 16 + threadIdx.x] are
- In fact,
Ais an 2D matrix; however, when copying from the host, it must be 1D. As a result, the 2D matrix is mapped to 1D array. Therefore, you need a formula to find an index in 1D to correctly choose an intended element you want from 2D matrix. row*Nchooses the row. For example,A[0][0]is equivalent toA[0*N].A[1][0]is equivalent toA[1*N].tile*16moves to the current tile since theAsandBscannot entirely fitAandB. For example,A[0][16]is equivalent toA[0*N + 1*16]becauseA[0][16]is in the second tile (tile 1) (don’t forget that the first tile is tile 0). To be a reference, the first tile contains elements from row 0 to row 15 and from col 0 to col 15 in our case that the size ofAsandBsis 16x16.threadIdx.xmoves to any element within 16 elements. For example,A[0][18]is equivalent toA[0*N + 1*16 + 2]because this element is the third element (don’t forget that the first element has an index 0) of the second tile (tile 1).
Pause here if you are now overwhelmed. I understand that this is difficult to wrap in your head.
In the same way, the reasons of being B[(tile * 16 + threadIdx.y) * N + col] are
- You now want to copy a column in
BtoBs tile*16is to select the current tile of your column.threadIdx.yis to select the correct element in the current tile.(tile*16 + threadIdx.y)*Nbecause when mapping 2D to 1D, it goes row-wise.colis to select the correct column.
I know this is more difficult to understand than mapping A. I hope this visualization helps you.
How to map from 2D array to 1D array
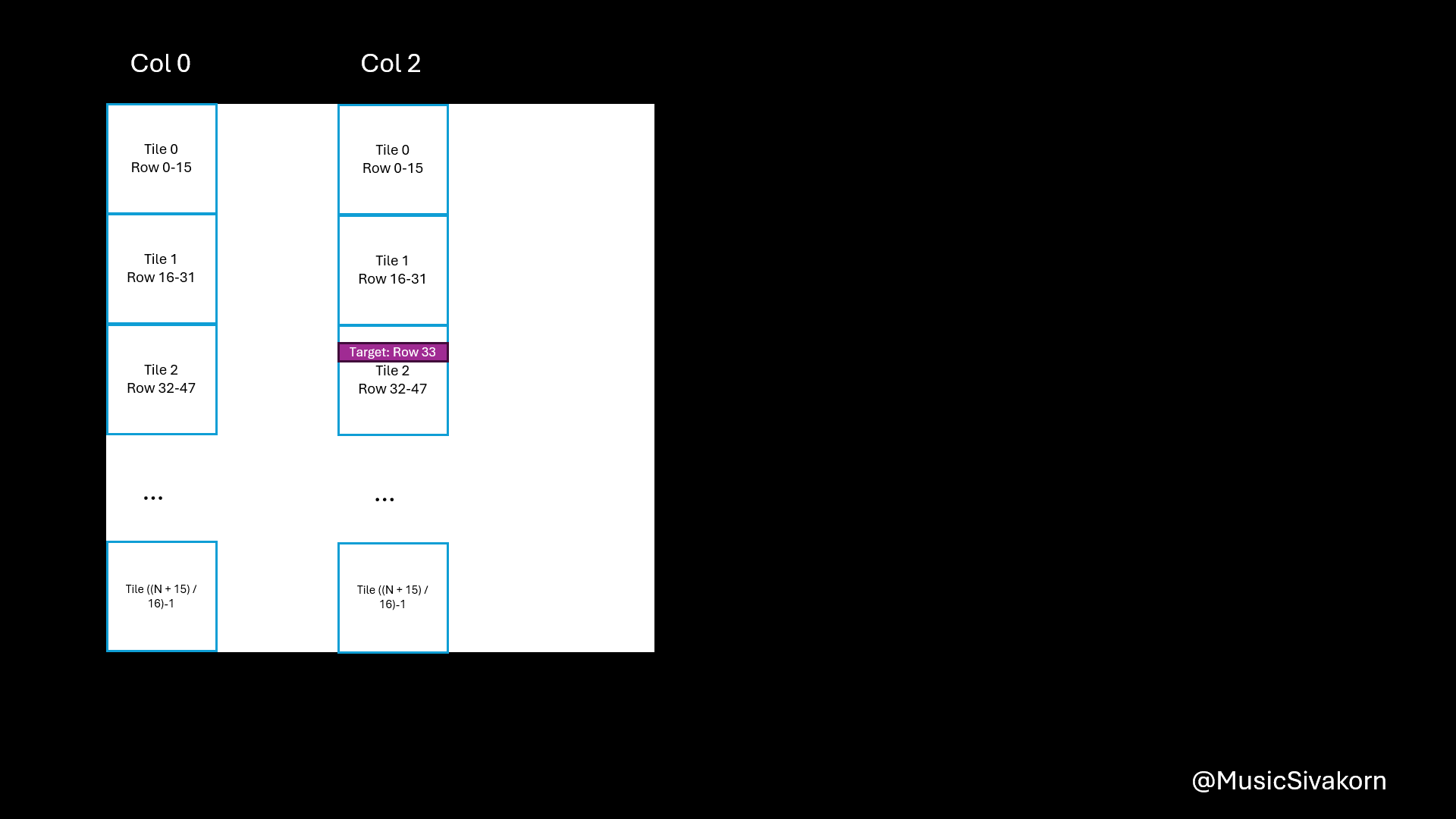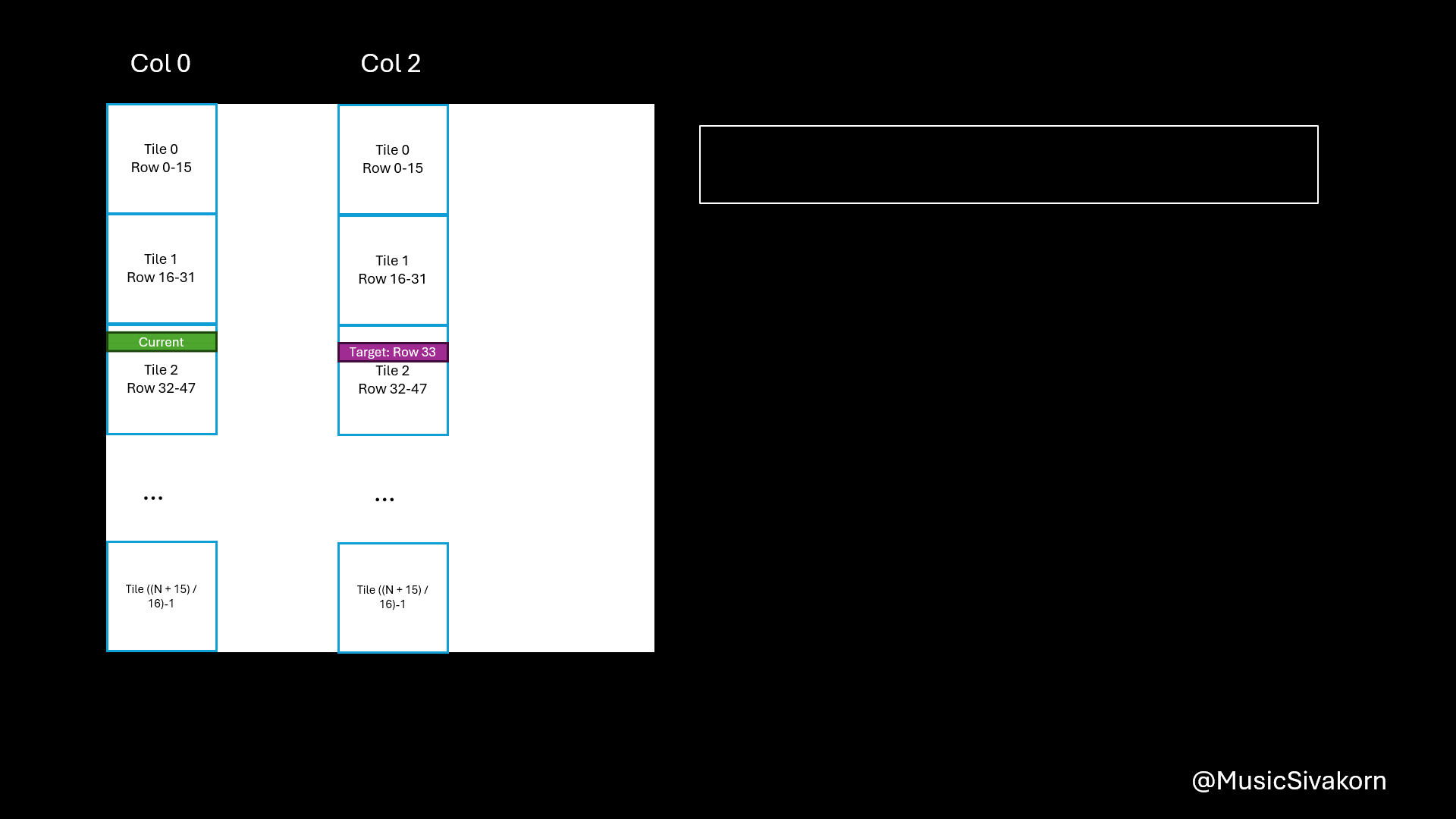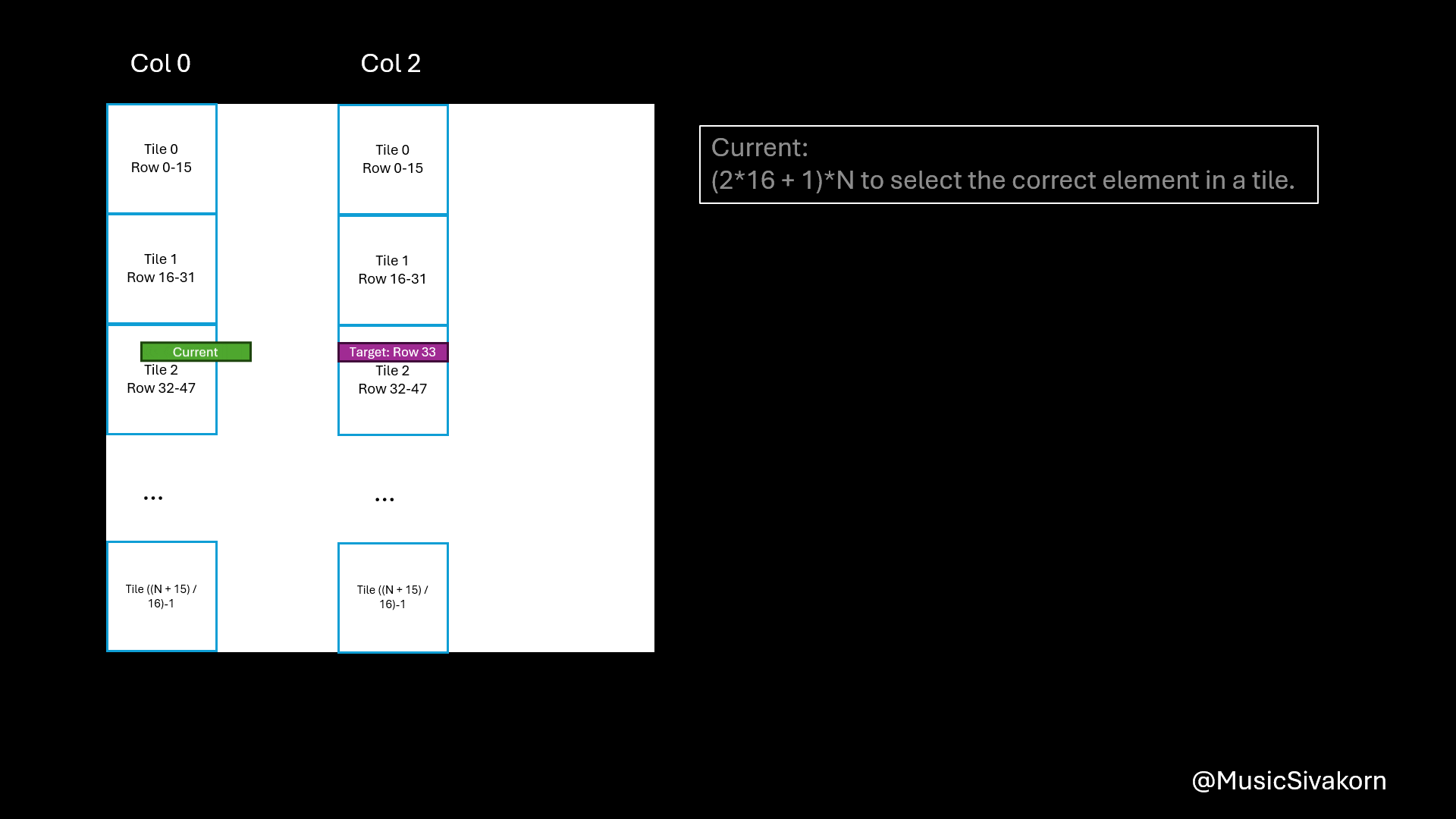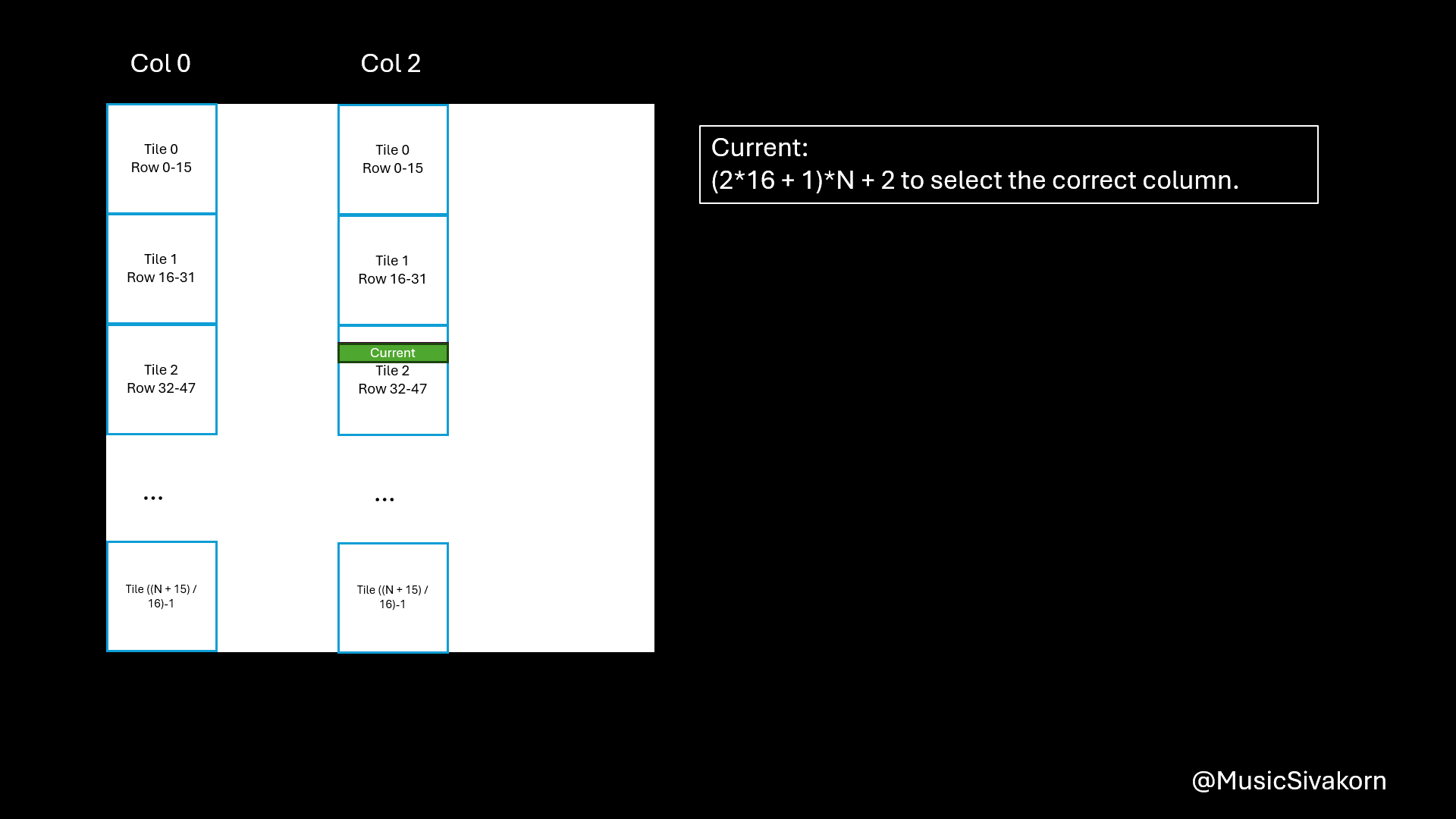An animation showing how to map B to Bs.
We need to wait until all elements in As and Bs are filled. Therefore, __syncthreads() is used to ensure that all threads finish their work before continuing to the next part in the code. Please note that adding this does not make the data copying becoming sequential. All threads can still work in parallel. This command just waits until all threads finish their work. If you still feel confused, let’s assume that each thread normally uses 1 second to finish copying data. However, something happens so that 2 of these threads uses 2 seconds. Using __syncthreads() makes the data copying part to use 2 seconds, due to the slow threads, not to use X seconds, where X is the number of threads.
After copying data to the matrices on the shared memory, you can do a multiplication by using matrices on the shared memory. You will get a partial result for each tile. You should add them to the current value of sum, which contains the result of the multiplication from all previous tiles. To be clearer, the variable sum has the partial multiplication result of the first 16 elements of the array A (A[0..15]) and B (B[0..15]) after finishing the first iteration (tile=0). Then, it will have the partial multiplication result of the first 32 elements of the array A and B after finishing the second iteration (tile=1) by adding the multiplication result of element A[16..31] and B[16..31] to the current sum having the result of the first 16 elements, and so on.
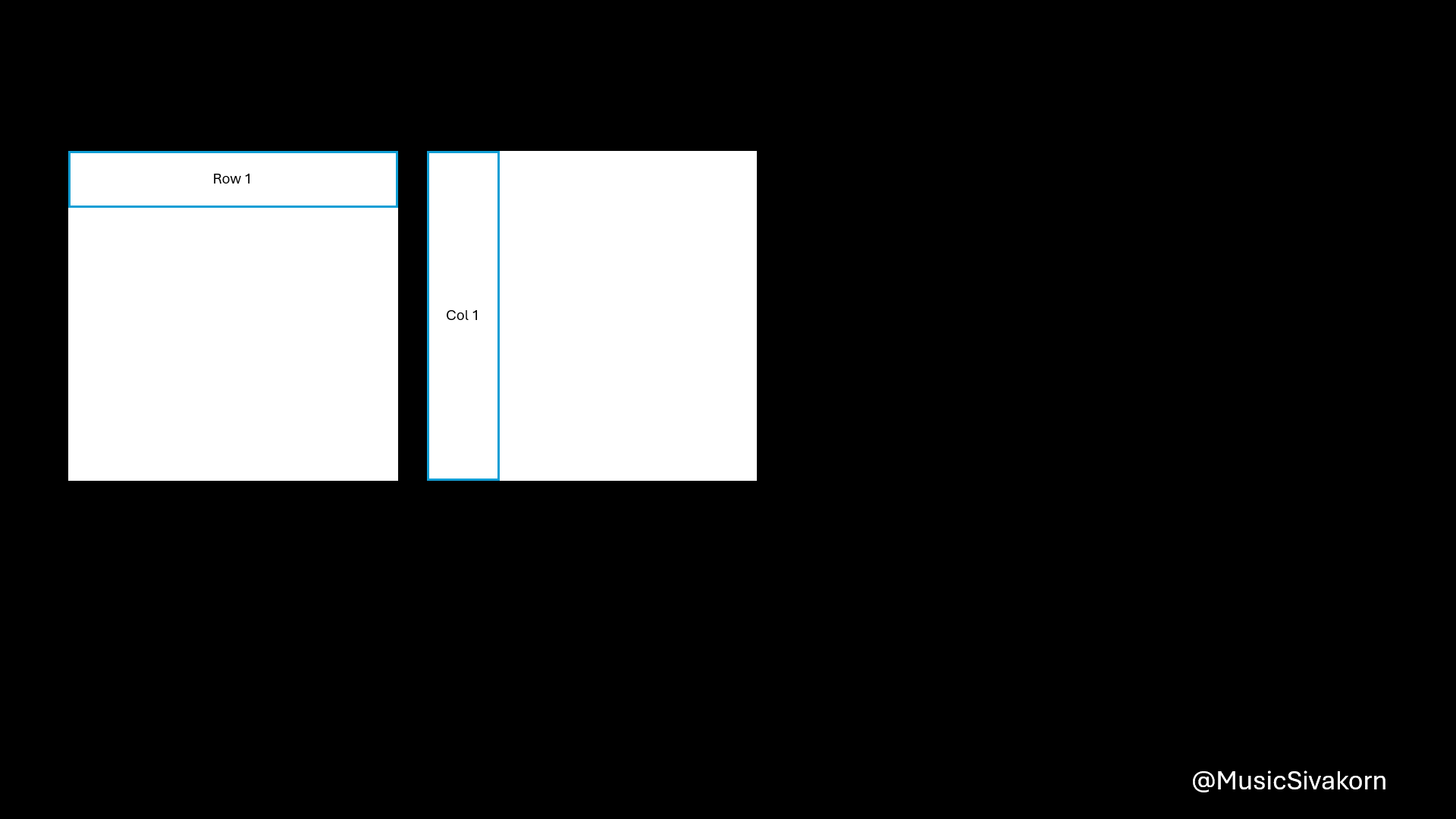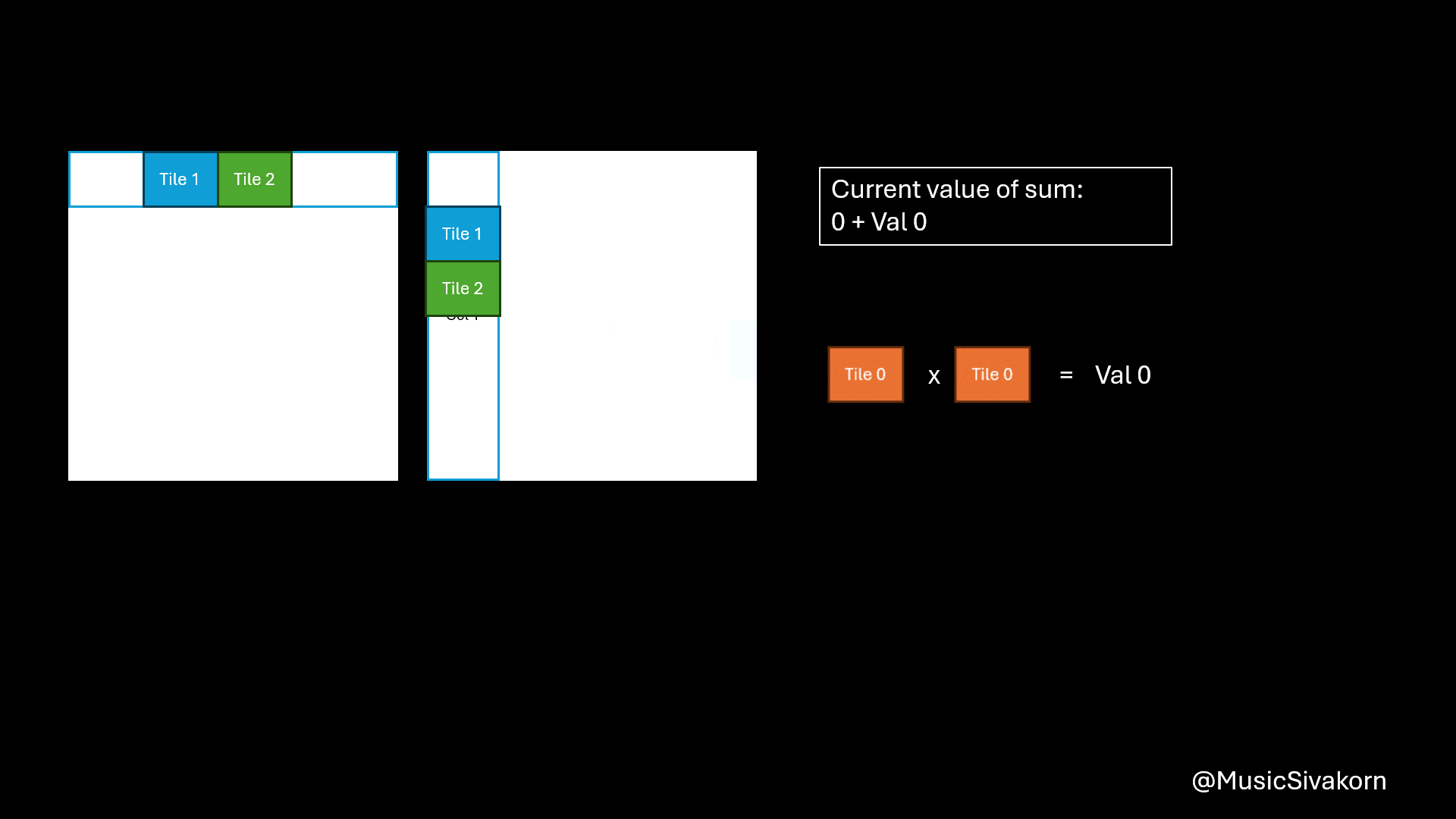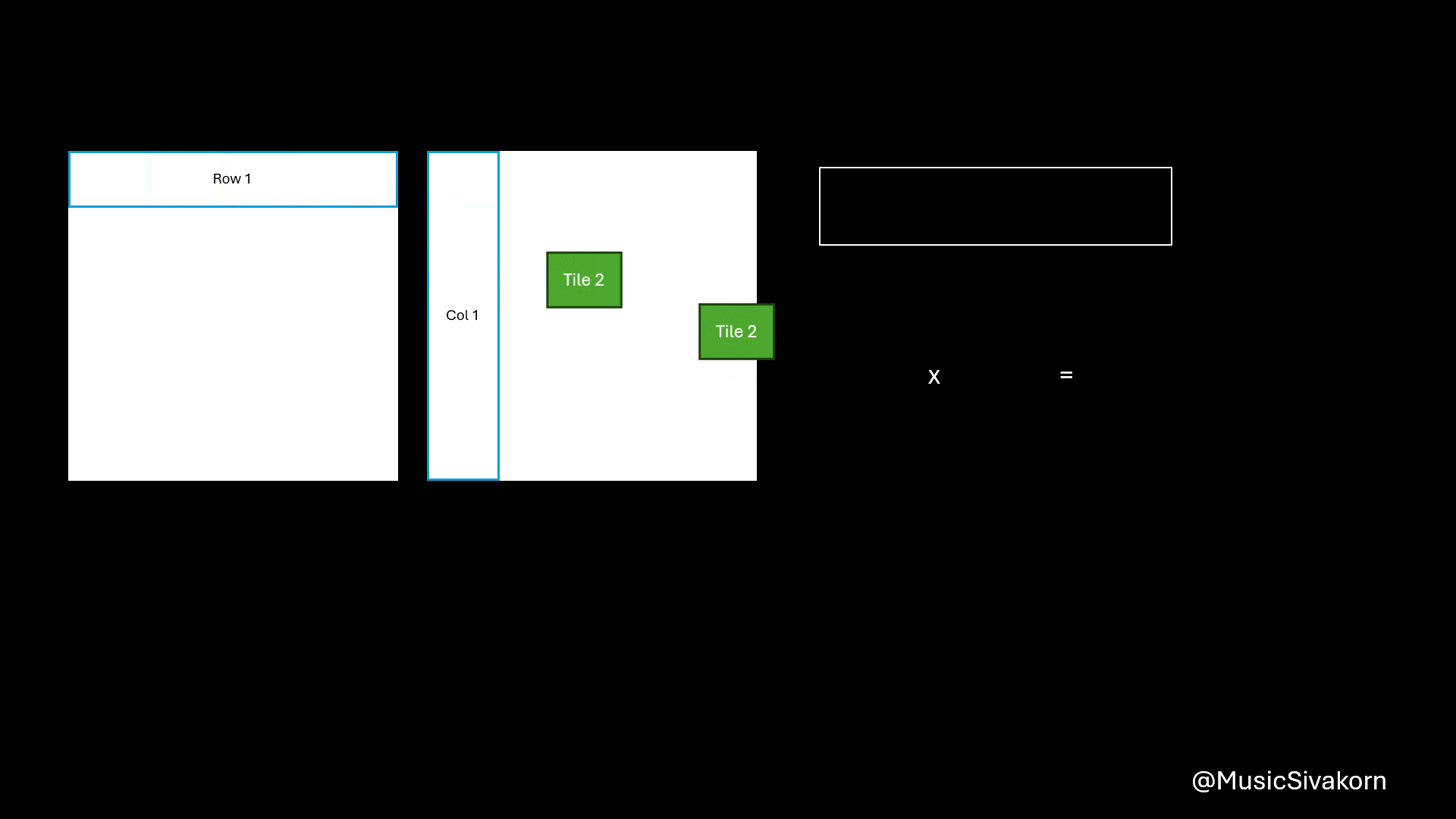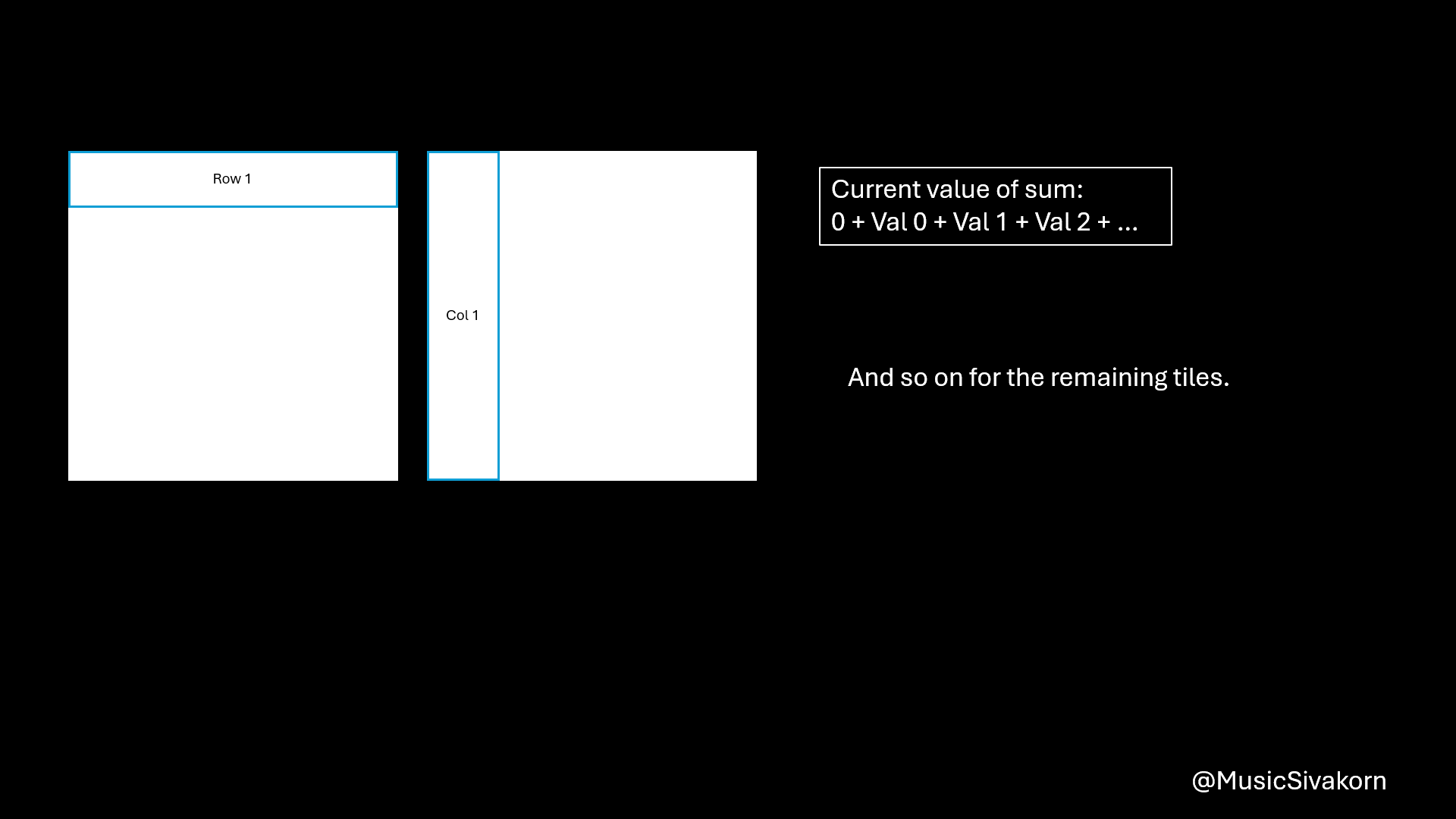Showing how to compute a matrix multiplication by combining several partial multiplication together.
Don’t forget to __syncthreads() before starting a new tile (continue to the next iteration of the loop) because you will not want to copying new set of data to the shared memory while the current iteration does not finish computing the multiplication result yet.
// Still inside the tile loop
__syncthreads();
// Compute using shared memory
for (int k = 0; k < 16; k++) {
sum += As[threadIdx.y][k] * Bs[k][threadIdx.x];
}
__syncthreads();
After finishing the loop, sum will have a complete matrix multiplication of a particular element. You can assign it to that element of the array C.
if (row < N && col < N) {
C[row * N + col] = sum;
}
After running the full code, this is the result.
Matrix multiplication: 512x512
Block size: 16x16, Grid size: 32x32
Performance Results:
==================
Global Memory Time: 0.643 ms
Shared Memory Time: 0.325 ms
Speedup: 1.98x
Results match: Yes (max diff: 0.000000)
✓ Shared memory is 1.98x faster!
You can see that using a shared memory has a speedup comparing to doing a multiplication by accessing data from the global memory.
Allocating Shared Memory Dynamically
From the matrix multiplication example, you see that I fix the allocated size on the shared memory to be 16x16. This is a static allocation. You know the required size at compile time. Therefore, it is simple to use.
__global__ void staticMem()
{
__shared__ int s[64]; // Fixed size of 64 integers
// ...
}
There is another way called a dynamic allocation. You determine the size at runtime.
__global__ void dynamicMem()
{
extern __shared__ int s[]; // Size determined at kernel launch
}
When launching a kernel, you do as below.
int n = 64;
dynamicMem<<<1, n, n*sizeof(int)>>>();
It is in the format of kernelName<<<numBlocks, numThreads, dynamicSharedMemSize>>>(); where numBlocks is the number of thread blocks, numThreads is the number of threads per thread block, and dynamicSharedMemSize is a size of dynamically allocated shared memory in bytes. dynamicSharedMemSize is optional, and its default value is 0. The dynamic allocation is more flexible since its size depends on runtime parameters. It is better for use cases that need varying amounts of shared memory.
However, you cannot use this method to create higher-dimension array. CUDA only allows a single 1D dynamic array declaration. If you want to use it for a higher-dimension, you need to map it to 1D index, as we have done in the matrix multiplication example.
Moreover, you cannot declare more than one extern __shared__ array per kernel. The following example is prohibited!
__global__ void badExample() {
extern __shared__ float As[];
extern __shared__ float Bs[]; // Error! Can't have multiple
}
But you can still mix the static and dynamic allocation together.
__global__ void mixedExample() {
__shared__ float As[16][16];
extern __shared__ float dynamic_mem[];
float* Bs = dynamic_mem; // Use dynamic for variable-size data
}
So, to summarize, here are some takeaways.
- All threads in a thread block can cooperate to solve a subproblem. See our matrix multiplication example!
- All threads in a thread block can access the same variable from the shared memory.
Coalesce Access to Memory
Coalesced memory access occurs when threads in a warp can access consecutive memory addresses in a way that GPU can use a fewer number of transactions to retrieve data from the memory.
When loading data, modern GPUs loads it as a block of memory called a cache line instead of loading just a single piece of data.
Let’s have a first example. Assuming that the cache line size is 128 bytes, if all threads in a warp wants to access an integer or float, which are 4 bytes, the most efficient method is when the GPU can use only one transaction to retrieve the cache line containing 32 4-byte values, and all 32 threads in the warp can use all values in that cache line.
In other words, for a coalesced access, GPU use only 1 memory transaction to serve data to all 32 threads in the warp, while up to 32 memory transactions are required if threads use a non-coalesced access.
Start Addr
Cache Line [0 | 4| 8| 12| ...| 120| 124]
Used by thread 1 2 3 4 ... 31 32
Okay. We now finish the first example.
Let’s have a more realistic second example. In modern GPUs, each memory transaction retrieves a 32-byte cache line. if GPU wants to provide 4-byte data (let’s assume to be int) to all threads in a warp, 4 memory transactions are required because 32 threads * 4 bytes = 128 bytes, which requires 4 32-byte cache line.
In a perfect coalescing scenario, each transaction fetches a cache line containing exactly 8 useful 4-byte data. All 32 byte in each cache line are used by threads in the warp.
Start Addr Byte
Cache Line #1 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 1 2 3 4 ... 7 8
Start Addr Byte
Cache Line #2 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 9 10 11 12 ... 15 16
Start Addr Byte
Cache Line #3 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 17 18 19 20 ... 23 24
Start Addr Byte
Cache Line #4 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 25 26 27 28 ... 31 32 <- 32th thread is a final Thread of a warp.
Note: Each cache line has 32 bytes, from byte 0 to byte 31. Each int takes 4 bytes. So, each cache line has 8 int. For example, the first int takes byte 0 to byte 3, and the second int takes byte 4 to byte 7. And so on.
However, if there occurs a misalignment so that the first 4-byte data of the first cache line is not the data requested by any threads in a warp, 5 memory transactions are required.
Start Addr Byte
Cache Line #1 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread - 1 2 3 ... 6 7
Start Addr Byte
Cache Line #2 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 8 9 10 11 ... 14 15
Start Addr Byte
Cache Line #3 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 16 17 18 19 ... 22 23
Start Addr Byte
Cache Line #4 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 24 25 26 27 ... 30 31
Start Addr Byte
Cache Line #5 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 32 - - - ... - - <- 32th thread is a final Thread of a warp.
Let’s have one more example, using the same 32-byte cache line scenario, what if each thread accesses every other element? How many memory transactions are required?
Start Addr Byte
Cache Line #1 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 1 - 2 - ... 4 -
Start Addr Byte
Cache Line #2 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 5 - 6 - ... 8 -
...
Start Addr Byte
Cache Line #8 [0 | 4| 8| 12| ...| 24| 28|] <- Fetch this use 1 memory transaction.
Used by thread 29 - 30 - ... 32 - <- 32th thread is a final Thread of a warp.
The answer is 8 memory transactions to fetch 8 cache lines.
So, the idea of coalescing access is that the GPU cannot fetch a partial cache line. If your threads need data that spans across multiple cache lines, you must fetch as full lines even if you only use a few bytes from some of them. Coalesced access means that you organize your memory access pattern so that you minimize the number of cache line fetching needed by maximizing the utilization of each fetched cache line.
Now, let’s see the real coding example. I use a matrix ADDITION to show this topic.
An Example Showing the Benefit of Using a Coalesced Access
#include <cuda_runtime.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// Simple matrix ADDITION example that benefits more from coalesced memory
__global__ void matrix_add_coalesced(float *A, float *B, float *C, int N) {
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
if (row < N && col < N) {
C[row*N + col] = A[row*N + col] + B[row*N + col];
}
}
__global__ void matrix_add_non_coalesced(float *A, float *B, float *C, int N) {
int col = blockIdx.y * blockDim.y + threadIdx.y; // SWAPPED
int row = blockIdx.x * blockDim.x + threadIdx.x; // SWAPPED
if (row < N && col < N) {
C[row*N + col] = A[row*N + col] + B[row*N + col];
}
}
int main() {
const int N = 512; // Smaller for clearer demonstration
size_t size = N * N * sizeof(float);
float *h_A, *h_B, *h_C_coalesced, *h_C_non_coalesced;
float *d_A, *d_B, *d_C_coalesced, *d_C_non_coalesced;
// Allocate host memory
h_A = (float*)malloc(size);
h_B = (float*)malloc(size);
h_C_coalesced = (float*)malloc(size);
h_C_non_coalesced = (float*)malloc(size);
// Initialize matrices
for (int i = 0; i < N * N; i++) {
h_A[i] = (float)rand() / RAND_MAX;
h_B[i] = (float)rand() / RAND_MAX;
}
// Allocate device memory
cudaMalloc(&d_A, size);
cudaMalloc(&d_B, size);
cudaMalloc(&d_C_coalesced, size);
cudaMalloc(&d_C_non_coalesced, size);
// Copy to device
cudaMemcpy(d_A, h_A, size, cudaMemcpyHostToDevice);
cudaMemcpy(d_B, h_B, size, cudaMemcpyHostToDevice);
dim3 blockSize(16, 16);
dim3 gridSize((N + 15) / 16, (N + 15) / 16);
// Timing
cudaEvent_t start, stop;
cudaEventCreate(&start);
cudaEventCreate(&stop);
printf("Matrix Addition: %dx%d\n", N, N);
printf("Block size: 16x16, Grid size: %dx%d\n\n", gridSize.x, gridSize.y);
// Time non-coalesced version
cudaEventRecord(start);
for (int i = 0; i < 10; i++) {
matrix_add_non_coalesced<<<gridSize, blockSize>>>(d_A, d_B, d_C_non_coalesced, N);
}
cudaEventRecord(stop);
cudaEventSynchronize(stop);
float non_coalesced_time;
cudaEventElapsedTime(&non_coalesced_time, start, stop);
non_coalesced_time /= 10; // Average over 10 runs
// Time coalesced version
cudaEventRecord(start);
for (int i = 0; i < 10; i++) {
matrix_add_coalesced<<<gridSize, blockSize>>>(d_A, d_B, d_C_coalesced, N);
}
cudaEventRecord(stop);
cudaEventSynchronize(stop);
float coalesced_time;
cudaEventElapsedTime(&coalesced_time, start, stop);
coalesced_time /= 10; // Average over 10 runs
// Copy results back
cudaMemcpy(h_C_coalesced, d_C_coalesced, size, cudaMemcpyDeviceToHost);
cudaMemcpy(h_C_non_coalesced, d_C_non_coalesced, size, cudaMemcpyDeviceToHost);
// Check correctness
bool correct = true;
float max_diff = 0.0f;
for (int i = 0; i < N * N && correct; i++) {
float diff = fabs(h_C_coalesced[i] - h_C_non_coalesced[i]);
max_diff = fmax(max_diff, diff);
if (diff > 1e-3) correct = false;
}
printf("Performance Results:\n");
printf("==================\n");
printf("Non-coalesced Memory Time: %.3f ms\n", non_coalesced_time);
printf("Coalesced Memory Time: %.3f ms\n", coalesced_time);
printf("Speedup: %.2fx\n", non_coalesced_time / coalesced_time);
printf("Results match: %s (max diff: %.6f)\n", correct ? "Yes" : "No", max_diff);
if (coalesced_time < non_coalesced_time) {
printf("\n✓ Coalesced memory is %.2fx faster!\n", non_coalesced_time / coalesced_time);
}
float bytes_transferred = 3.0f * size; // Read A, B; Write C
float coalesced_bandwidth = (bytes_transferred*1e-9) / (coalesced_time * 1e-3);
float non_coalesced_bandwidth = (bytes_transferred*1e-9) / (non_coalesced_time * 1e-3);
printf("Coalesced Bandwidth: %.2f GB/s\n", coalesced_bandwidth);
printf("Non-coalesced Bandwidth: %.2f GB/s\n", non_coalesced_bandwidth);
// GFLOPS calculation
long long operations = (long long)N * N; // 1 add per element
double gflops_non_coalesced = (operations * 1e-9) / (non_coalesced_time * 1e-3);
double gflops_coalesced = (operations * 1e-9) / (coalesced_time * 1e-3);
printf("GFLOPS (Coalesced): %.2f\n", gflops_coalesced);
printf("GFLOPS (Non-coalesced): %.2f\n", gflops_non_coalesced);
// Cleanup
cudaEventDestroy(start);
cudaEventDestroy(stop);
cudaFree(d_A); cudaFree(d_B); cudaFree(d_C_coalesced); cudaFree(d_C_non_coalesced);
free(h_A); free(h_B); free(h_C_coalesced); free(h_C_non_coalesced);
return 0;
}
To execute this code,
- Save it as
matrix_coalesce_demo.cu - Run
nvcc -o matrix_coalesce_demo matrix_coalesce_demo.cu - Run
./matrix_coalesce_demo
Both matrix_add_non_coalesced and matrix_add_coalesced compute the same result, but differ in memory access efficiency.
At a first sight, you may think that these two versions, matrix_add_non_coalesced and matrix_add_coalesced, provide a same set of (row,col) for each thread block. For example, the thread block 0 of both functions produce
(0,0), (0,1), ..., (0,15)
.
.
.
(15,0), (15,1), ..., (15,15)
Note that each thread block has a size of 16x16 and the index starts from 0.
However, the difference, which brings about a significant difference of performance, is how threads are grouped into each warp. CUDA assigns thread IDs in row-major order within a block: threadIdx.x changes fastest, then threadIdx.y, then threadIdx.z.
for (int y = 0; y < threadIdx.y; y++)
for (int x = 0; x < threadIdx.x; x++) // Innermost -> Change fastest
So, in a matrix_add_coalesced version,
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
- Thread 0: row=0, col=0 -> Access
A[0*N + 0] - Thread 1: row=0, col=1 -> Access
A[0*N + 1] - Thread 2: row=0, col=2 -> Access
A[0*N + 2] - And so on
These are consecutive memory locations, which can be easily combined into 1 memory transaction.
However, in a matrix_add_non_coalesced version,
int col = blockIdx.y * blockDim.y + threadIdx.y;
int row = blockIdx.x * blockDim.x + threadIdx.x;
- Thread 0: row=0, col=0 -> Access
A[0*N + 0] - Thread 1: row=1, col=0 -> Access
A[1*N + 0] - Thread 2: row=2, col=0 -> Access
A[2*N + 0] - And so on
These are N elements apart (different rows), which can finally be on different cache line, requiring several separated memory transactions.
The idea is that the coalesced access is about construction. The GPU does not care about the final result. It focuses on the memory access method. If 4 threads are requesting for memory address [100, 101, 102, 103], it is likely that this request can be combined into a single transaction, while 4 threads requesting for memory address [100, 1124, 2148, 3172] is unlikely to be combined to a single transaction, and several transactions are required.
Finally, this is the result of running this script.
Matrix Addition: 512x512
Block size: 16x16, Grid size: 32x32
Performance Results:
==================
Non-coalesced Memory Time: 0.430 ms
Coalesced Memory Time: 0.022 ms
Speedup: 19.54x
Results match: Yes (max diff: 0.000000)
✓ Coalesced memory is 19.54x faster!
Coalesced Bandwidth: 142.88 GB/s
Non-coalesced Bandwidth: 7.31 GB/s
GFLOPS (Coalesced): 11.91
GFLOPS (Non-coalesced): 0.61
A function using a coalesced access is faster than a that of non-coalesced access.
This is the end of this part! Before finishing this part, let’s have some takeaways.
- GPU scheduling is based on warps. You can maximize warps in SM to hide memory access latency.
- Use
__syncthreads()to wait until all threads finish their work. One usecase is to have it between filling up shared memory and starting to use it. - Utilize a shared memory to increase performance.
- Try to use a coalesced memory access.
The next part will discuss how to use CUDA stream to run several kernels asynchronously, which can make your CUDA program even faster since it can process more data at the same time!
If you enjoy this blog, you can support me with a cup of coffee. Thank you for reading until here and see you then!
This blog is inspired from Lecture 7 of Low-Level Parallel Programming course offered by Uppsala University.